Übung 25.06.09

Aufgabe 18: Schwingungen schriftlich (3 Punkte)
Ein Feder-Masse-Pendel der Masse m = 0, 5 kg führe eine ungedämpfte harmonische
Schwingung aus mit einemWeg-Zeit-Verhalten entsprechend y(t) =A*sin(ωo*t + φo), worin
A = 25 cm (Amplitude), ωo = 4π Hz (Kreisfrequenz), und φo=π/5 (Nullphasenwinkel).
Berechnen Sie:
1. Die Auslenkung, die Geschwindigkeit, die Beschleunigung zum Zeitpunkt t = 1; 325 s
2. Die maximal erreichbaren Werte fur die Beschleunigung und die Geschwindigkeit
(mit Rechenweg bzw. guter Begründung der Werte).
3. Die Energie des Pendels. (Denken Sie sich hierbei das Pendel reibungsfrei auf dem
Erdboden, horizontal schwingend.)
Hinweis: Denken Sie an die richtige Taschenrechner-Einstellung.
Lösung:

1.)

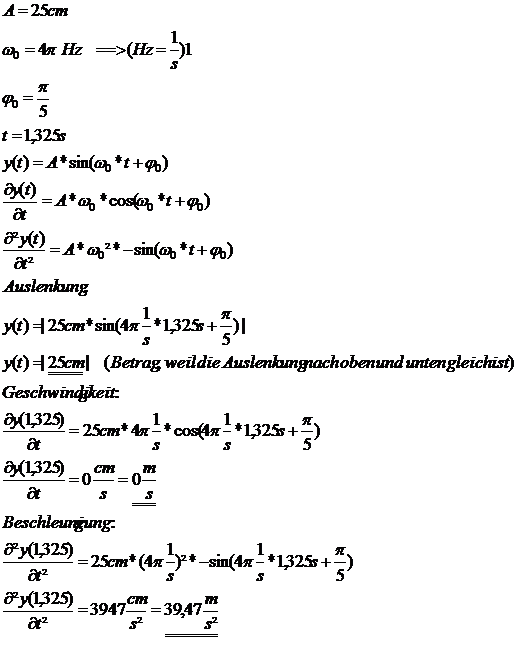
2.)Die erste Ableitung der Funktion gibt die Momentangeschwindigkeit der Funktion an, an dem HP der 2.Ableitung ist die Geschwindigkeit maximal. Den Hp berechnet man wenn man wiederrum die 2.Ableitung ableitet und Null setzt. Intuitiv ist der Hp der Ableitung bei der Wendestelle der Funktion, diese ist dort wo der Graph die t-Achse (Ordinate) schneidet. (Bei der Rechnung Taschenrechner auf "Rad") Man kann auch bei dem 2. Teil mit π/2 = ωo*t + φo rechnen, da sich die Schwingungen immer wiederholen.

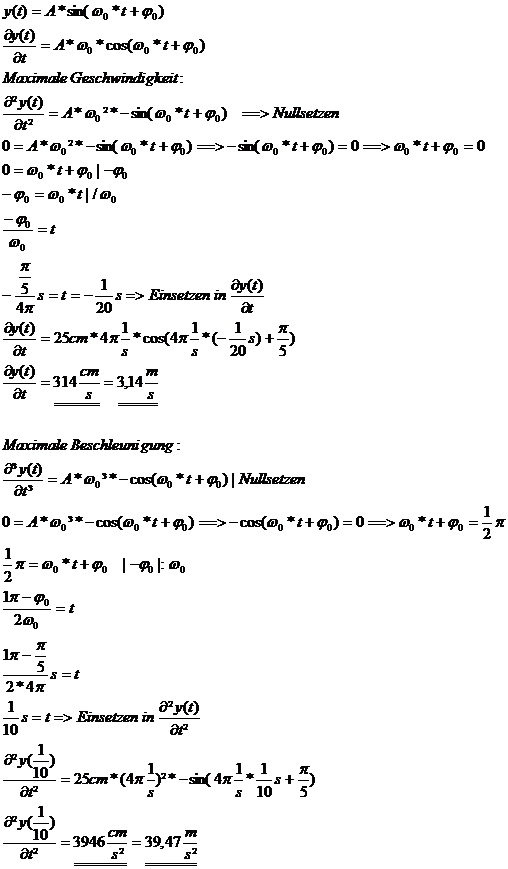
3.)

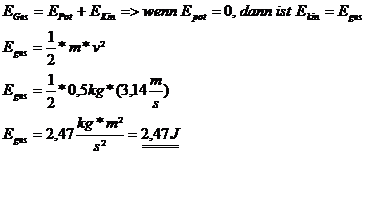
Aufgabe 19: Welle
Ein Krankenwagen nähere sich mit eingeschaltetem Martinshorn einer Unfallstelle. Für
die dort unbeweglich Wartenden gilt im Vergleich zu den Mitfahrenden des Wagens:
1. Sie hören einen höheren Sirenenton
2. Sie hören einen gleichhohen Sirenenton
3. die Schallwelle, die sie erreicht hat eine niedrigere Frequenz
4. die Schallwelle, die sie erreicht hat eine kürzere Wellenlänge
5. eine Aussage über die sie erreichende Wellenlange ist nicht möglich
Begründen Sie Ihre Antwort.

Lösung:

Vor dem Krankenwagen: λv = c *T − v *T ==> geringere Frequenz ==> höherer Ton
Hinter dem Krankenwagen: λh = c *T + v *T

Verständnisaufgabe 25: Schwingungen schriftlich (1 Punkt)
Für ein Uhrenpendel, dessen Antrieb ausgesetzt hat, trift folgender zeitlicher Verlauf der
kinetischen Energie zu:

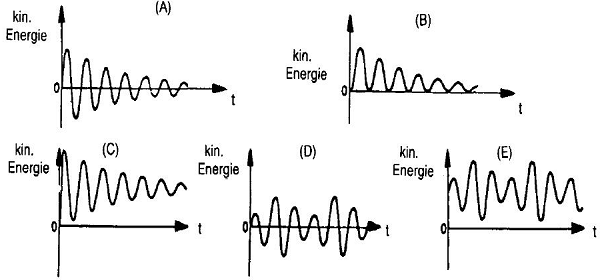
1. Diagramm A
2. Diagramm B
3. Diagramm C
4. Diagramm D
5. Diagramm E

Lösung: Die Potentielle und Kinetische Energie geht immer mehr in Reibungsenergie und den Antrieb der Uhr "verloren" deshalb sinkt das Energieniveau des Pendels gleichmäßig. ==> Diagramm B

Verständnisaufgabe 26: Schwingungen
Wo wird eine ungedämpfte Schwingung dargestellt?

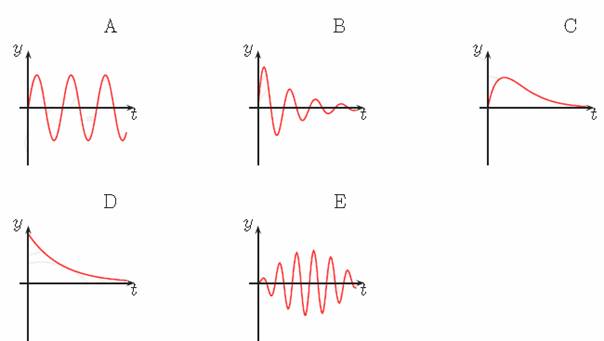
1. Diagramm A
2. Diagramm B
3. Diagramm C
4. Diagramm D
5. Diagramm E

Verständnisaufgabe 27: Schwingungen
Beim Durchgang durch die Ruhelage (gestrichelt gekennzeichnet)
einer harmonisch schwingenden Masse gilt für die Beträge
der Geschwindigkeit v und der Beschleunigung a:
1. a und v sind maximal
2. a = 0 und v = 0
3. a ist maximal und v = 0
4. a = 0 und v ist maximal
5. a und v nehmen gerade die Hälfte ihrer Maximalwerte an